Well-definition

In mathematics, well-definition is a mathematical or logical definition of a certain concept or object (a function, a property, a relation, etc.) which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy the required properties. Sometimes however, it is economical to state a definition in terms of an arbitrary choice; one then has to check that the definition is independent of that choice. On other occasions, the required properties might not all be obvious; one then has to verify them. These issues commonly arise in the definition of functions.

For instance, in group theory, the term well-defined is often used when dealing with cosets, where a function on a coset space is often defined by choosing a representative: it is then just as important that we get the same result regardless of which representative of the coset we choose. As an example, take the definition:

f(x₁)=f(x₂) if x₁~x₂

then the definition makes sense, and f is well-defined on X/~. Although the distinction is often ignored, the function on X/~, having a different domain, should be viewed as a distinct map 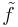$\tilde{f}$ .

As an example, consider the equivalence relation between real numbers defined by θ₁~θ₂ if there is an integer n such that θ₁-θ₂ = 2πn, where π (not italicized) denotes Pi. The quotient set X/~ may then be identified with a circle, as an equivalence class [θ] represents an angle. (In fact this is the coset space R/2πZ of the additive subgroup 2πZ of R.) Now if f:R→R is the cosine function, then $\tilde{f}([\theta])=\cos\theta\!$ is well-defined, whereas if f(θ) = θ then $\tilde{f}([\theta])=\theta$ is not well-defined function; in other words, it is a multivalued function.

Two other issues of well-definition arise when defining a function f from a set X to a set Y. First, f should actually be defined on all elements of X. For example, the function f(x) = 1/x is not well-defined as a function from the real numbers to itself, as f(0) is not defined. Secondly, f(x) should be an element of Y for all x∈X. For example, the function f(x) = x² is not well-defined as a function from the real numbers to the positive real numbers, as f(0) is not positive.

A set is well-defined if any given object either is an element of the set, or is not an element of the set.

1 Notation using ↓ and ↑
2 Undefined values
- 2.1 The symbols of infinity
- 2.2 Undefined forms of exponentiation
3 Singularities in complex analysis
4 See also

Notation using ↓ and ↑

In computability theory, if f is a partial function on S and a is an element of S, then this is written as f(a)↓ and is read "f(a) is defined."

If a is not in the domain of f, then f(a)↑ is written and is read as "f(a) is undefined".

Undefined values

In common mathematical usage, an arithmetic expressionE(x,y,...) is called undefined for certain values x₀, y₀,... of the variables x, y, ... in two different cases:

A meaning for E(x₀,y₀,...) has not been specified in the definition of E.
The same, and in addition there is no "sensible" way to extend the existing definition to cover the case x₀,...

One very common case of what "sensible" can mean is in the context of continuous functions. For instance, the real-valued function f(x) = (2x)/x is undefined for x = 0 (because the denominator becomes zero), but it can be extended continuously by defining f(x) = 2 for all real x. On the other hand, the function q(x,y) = x/y is defined for any real number x and any real number y different from 0. It is undefined for y=0 and cannot be extended continuously to any point (x,0). This is expressed in short by: you cannot divide by zero.

The symbols of infinity

In analysis, measure theory, and other mathematical disciplines, the symbol ∞ is frequently used to denote an infinite pseudo-number, in real analysis alongside with its negative -∞. The symbol has no well-defined meaning by itself, but an expression like a_n → ∞ is a shorthand for a divergent sequence which is eventually larger than any given real number.

Arithmetic with the symbols ±∞ is undefined. The following conventions of addition and multiplication are in common use:

∞ + x = ∞ for all reals x and x = ∞, -∞ + x = -∞ for all reals x and x = -∞
x ∞ = ∞ for positive reals x>0.

No sensible extension of addition and multiplication with ∞ exist in the following cases:

∞ - ∞
0 ∞ (although in measure theory, this is often defined as 0)
∞/∞

Undefined forms of exponentiation

The operation of exponentiation, a^b, is defined for all natural numbers b as an iterated product. If a ≠ 0, one defines a^-b as 1/a^b for b>0 and a⁰ = 1. The expression 0^b is undefined for b ≤ 0, although a common convention is to define 0⁰ as 1.

For rational exponents b=p/q and real positive basis a, the power a^b is defined as the qth root of a^p; this can be extended continuously to all real exponents b. If a < 0, there is no sensible definition of the power.

Singularities in complex analysis

In complex analysis, a point x where a holomorphic function is undefined is called a singularity. One distinguishes between removable singularities (the function can be extended holomorphically to x, poles (the function can be extended meromorphically to x), and essential singularities, where no meromorphic extension to x exists.